制粒机是饲料加工的主要机械之一,环模是制粒机的关键零部件,其打孔率决定了饲料加工的产量和生产成本。为了降低生产成本,提高生产效率,很多学者对环模进行了研究。文献对饲料制粒机压辊线磨损度进行了理论研究;文献分析得到了3种类型环模孔沿轴向路径的应力与变形分布,找到了环模孔倒角与环模孔轴向路径的应力与变形的影响关系。文献研究了环模孔受力简化模型,并基于简化模型对环模孔口进行了有限元受力分析。但对于环模上打孔的数量多少,目前主要采用经验类比的方法,无系统的设计方法。如采用有限元分析,由于大量孔的存在,环模的有限元分析难以实现,而采用等效弹性模量方法使得环模的有限元分析变为可能。等效弹性模量方法在多孔材料的力学分析中应用较多,如金属蜂窝夹芯板、非规则多孔介质材料、金属拱形波纹屋面和水力压裂中多孔岩体的力学分析中均有报道,但对环模这种多孔零件尚无报道。
为此,本文从环模的受力和等效弹性模量的角度出发,采用有限元方法对制粒机环模进行设计,并实验验证设计结果可靠性。
1、制粒机环模受力分析
颗粒饲料的加工中,环模制粒机是关键的核心设备,环模(如图l所示)是压制颗粒饲料的核心工作部件,其工作性能直接影响制粒的质量以及生产率,同时环模也是制粒机中最易磨损的部件之一。为了保证颗粒产品的性能,必须研究环模结构力学性能。研究环模和压辊之间的载荷分析对环模和压辊的结构设计具有很好的指导意义。
 假如电机满负荷工作,以1个环模和2个压辊的系统为例进行分析,如图2所示。
假如电机满负荷工作,以1个环模和2个压辊的系统为例进行分析,如图2所示。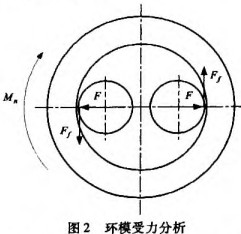
环模受到的转矩为
T=9546p/n
转换为环模驱动力为
Q= 2TR=吾=9 549 xPD (2)
压辊的挤压力为
F=q/f=9546p/ndf (3)
式中P-电机传递给环模的功率;
D-环模内径;
n一环模转速;
f-饲料与环模的摩擦因数。
作用在环模上的面积力p为
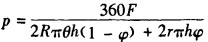
式中 R-环模半径;
r-孔半径;
θ一环模压力角;
a一环模开孔率;
h-环模厚度。
2、环模等效模型的弹性模量确定
采用有限元分析方法分析环模在均匀载荷与非均匀载荷时的应力强度情况,可以对传统的计算和分析方法设计结果进行修正,增加开孔率;但直接对多孔环模进行有限元分析对计算机提出了很高要求,甚至由于多孔的割裂作用,不能得到所需要的解。采用等效弹性模量方法将多孔结构的环模等价于一个实心环模可使得问题变得可解。
以虾料环模为例,采用传统的计算和分析方法设计,其直径420mm,孔径1.8mm,共有313 840孔,开孔率19.6%。图3为取含有9个孔的环模部分结构,将其等价为均质体单元,如图4所示。
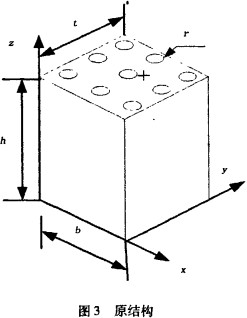
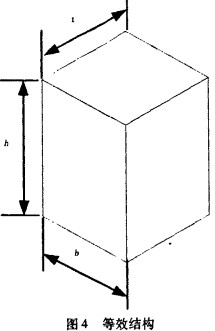
在图3所示的结构单元的:方向施加拉力载荷P,对于图3有

为了验证等效弹性模量的有效性,分别建立图3和图4的有限元分析模型,结果如图5和图6所示。从图5和图6可以看出,原始模型和等效模型的应力和变形几乎相等,可以说等效模型有效。

3、环模等效模型有限元分析
根据上面分析,多孔环模可以等效一个实心的环模。为研究问题的方便,载荷只考虑静载荷。在环模和物料接触的圆柱内表面施加载荷,如图7所示。
本文研究内直径420mm,孔径1.8mm,有效宽度185mm的虾料环模,所用材料为42CrMo。材料参数如表1所示。

模型材料等效弹性模量E= 19 400MPa。在环模一端施加固定约束,在两个压辊作用区域施加均布载荷,如图8所示。划分单元大小为10。仅考虑压辊和环摸接触处的压力,忽略孔内压力和摩擦力。设线速度大小为Im/s,压力载荷大小为=129 916N,载荷作用面积为2 492mm2,将载荷转换成均布面载荷,大小为52. 116MPa。
依次改变环模的弹性模量,进行有限元分析,求解应力和应变,得到环模的应力图和依弹性模量大小排列的应变等值线图,这里只给出一种弹性模量下的应力和应变图,如图9和图10所示。
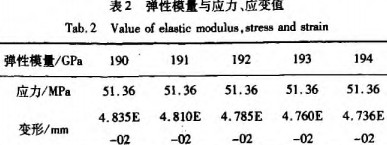
从应力图9中看出,大部分材料所受应力值远小于材料的许用应力;可以说当前环模模孔尺寸下,环模的材料强度有很多赘余,可以提高现有环模的开孔率;从变形图中看出,变形不大。从应力、应变图中提取最大应力和最大应变值列入表2,根据表2中内容绘制的弹性模量和应力和应变线性关系如图11和图12所示。从图11看出环模最大应力与弹性模量大小无关,而最大应变受弹性模量影响,且成线性关系,如图12所示。
4、环模结构尺寸优化
关于环模应变大小的确定,目前无依据可查,在本文中做这样一个尝试,即给定一个应变值,从图12中找出对应的环模等效弹性模量,进一步确定开孔率。这样的结果,环模既能满足强度要求,也能满足应变要求,同时又能提高开孔率。比如环模允许变形为4. 736E - 02mm,弹性模量为190GPa,应力为51. 36MPa。根据公式(7)来确定的环模有效面积为382.5mm2。进~步确定在原始单元上可打孔的数量为12个,比原型环模在同样面积上多打孔3个;从整体上看,比原环模孔数量13 840多出4 613,提高出孔率为23%。
5、结论
本文给出环模受力的解析表达,定义了环模的等效弹性模量,验证了等效弹性模量的有效性。对环模等效模型的受力和变形进行了分析,得出应力和应变与弹性模量之间的关系。根据应力和应变与弹性模量之间的关系和环模等效弹性模量公式,对现有环模结构尺寸进行了优化,优化后的环模在保证强度的前提下,比原型环模多打孔4136个,提高出孔率23%,为提高颗粒料产量提供设计依据。




