3.4生物质塑性变形理论
生物质秸秆
颗粒燃料的致密成型,物料在模具里受挤压后发生几何形状的改变,不能忽略,为几何非线性问题。考虑在实际应用中的大应力、大应变问题,本文应用大应变理论弹塑性有限元法分析问题。
对于生物质秸秆颗粒燃料致密成型的塑性变形,可以把秸秆原料看作“可压缩的连续体”,简化问题,应用塑性力学的理论分析变形问题。对变形作以下假设:
1)静水压力影响。生物质秸秆压缩变形实验表明,静水压力是其致密成型的重要条件,它可使生物质秸秆等可压缩材料产生塑性变形。
2)体积变化。生物质秸秆在塑性变形过程中,由于原料内部孔隙受到挤压闭合,体积缩小,密度增大,对于微小的生物质颗粒遵循体积不变原则,但对整个变形就不遵循体积不变条件了。
3)质量不变。生物质秸秆在压缩塑性变形时,虽然过程中受力很复杂,总的体积变小了,但是物料的密度也变大,整体的质量没有发生改变。
生物质塑性变形理论主要包括:屈服准则、强化准则、流动准则三种。
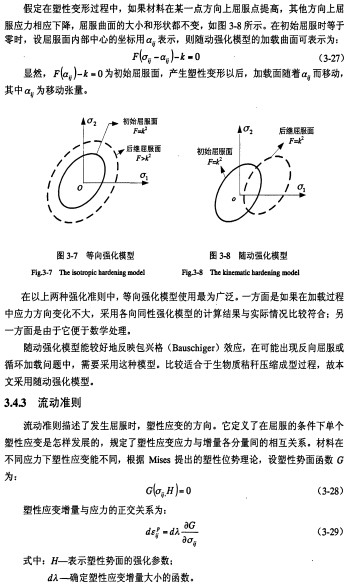
3.4.1屈服准则
屈服准则又称塑性条件,它是判断材料处于弹性阶段还是处于塑性阶段的准则。单向受力时,当应力小于材料屈服点时,材料处于弹性状态。当应力大于材料的屈服点时,材料由弹性状态进入塑性状态。在复杂应力状态时,物体内某一点发生塑性变形时,只有当各应力分量之间满足一定时,质点才开始进入塑性状态,这就是复杂应力下的屈服条件,也称塑性条件。
屈服准则是描述受力物体在复杂应力状态下质点进入塑性状态所遵守的力学条件,如果以应力a作为坐标轴,并建立一个多维坐标空间,这种力学条件一般可表示为:
F(%)=0 (3-18)
式中,称为屈服函数。
在三维应力空间中,当,(ax) <0时,此点落在屈服面内,说明是弹性变形;当F()-0时,此点落屈服面上,说明是塑性变形。
在生物质秸秆压缩致密成型过程中,材料弹塑性变形理论的关键内容是选择并建立屈服准则。在本文研究中,对生物质秸秆可压缩变形的屈服准则的建立可作以下假设:
1)将秸秆物料看作可压缩的连续体;
2)静水压力位于屈服面上;
31纯剪状态点位于屈服面上。
将生物质秸秆看作是可压缩的连续体,所以在受力时,秸秆内的应力变化是连续的,由于压缩体的屈服状态受静水应力影响,假设Q为纯剪切状态点、P为静水应力点,则连接P、Q两点的曲线如图3-4所示。
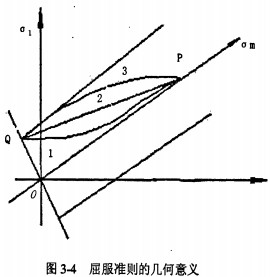
图中三条曲线分别代表的对象各不相同,曲线1是内凹的,是不可能的,因为在塑性加工理论中屈服表面处处外凸。曲线2是直线代表土力学或岩石的压缩成型特性。曲线3代表粉末体压缩成型特性,由于对称的原因,曲线3所形成的屈服表面,在主应力空间必然是与三个坐标轴等倾斜的回转面,其回转轴线为am方向。根据赵东等研究,生物质秸秆的压缩致密成型可近似为可压缩材料的屈服面曲线3。
常用的屈服准则有:特雷斯卡( Tresca)准则;米泽斯(Mises)准则;德鲁克.普拉格( Drucker-prager)准则;莫尔.库仑(Mohr coulomb)准则。
特雷斯卡准则的假设是材料屈服取决于最大剪力,其屈服条件可写为:





3.6本章小结
本章中,介绍了有限元知识及ANSYS有限元分析软件。对生物质致密成型过程的塑性变形、几何非线性等问题进行了分析,介绍了包括增量法、全量法、混合法等几种非线性求解方法。
通过研究生物质散粒体成型与金属粉末成型和土体性质有相似之处,在生物质原料成型过程研究中融入了流变学理论知识,加深了生物质致密成型理论上的分析研究,丰富了成型理论知识。
对生物质弹塑性变性理论进行了研究,介绍屈服准则、强化准则、流动准则。对生物质挤压有限变形采用欧拉法进行了研究。
选用了适合生物质秸秆的Druker-Prager屈服条件,根据致密成型中静水压力及屈服条件的影响,推导出弹塑性本构方程。同时依据平面应变的特点,建立平面应变的本构方程。
三门峡富通新能源销售
颗粒机、
秸秆压块机、饲料颗粒机、木屑颗粒机等生物质燃料饲料成型机械设备,同时我们还有大量的生物质颗粒燃料出售。







