1、前 言
大型轴流引风机是火力发电厂的主要辅机,它的性能好坏直接关系到电厂的安全性、经济性,目前300 MW火电机组上采用的锅炉引风机多为竖直方向进气的轴流引风机。该引风机的进口段是形状复杂的进气箱,进口截面为矩形,出口截面为圆形,即它的几何形状为一变截面的900弯道,再加上绕流轴套,故其内部流动非常复杂。关于进气箱内的流动细节以及引起的不均匀流动等方面的研究除文献外,见诸报道的论文较少。诸如进气箱的结构和前导叶形式、位置等来流条件将较大程度地影响引风机中的流动结构和性能。在CFD技术飞速发展的今天,数值计算的手段可以比较好地指导对引风机的设计、改造工作。
本文围绕某电厂轴流引风机中流动特性进行探讨。采用数值计算的手段对带前后导叶的轴流引风机中的内流问题进行研究,尤其对复杂进气箱中的流动特点进行分析,来说明进气箱的复杂形状和配套的轴套结构对流动性能的影响,所得结果为更好的结构改进提供参考。另外,对叶轮进口预旋形式和前导叶位置的影响等问题进行分析,旨在找到合理的方案。并利用相应的实验数据对数值计算的精度予以说明。
2、结构特点
本文研究的轴流引风机为动叶可调式,其叶轮外径为2.88 m,轮毂直径为1.8 m,叶片为翼型,设计工况下的安装角为380,叶片数为30;设置前导叶16片,采用两段圆弧加直线段的结构,进口采用负预旋;后导叶27片,单圆弧结构。该引风机是从竖直方向进气,经复杂的进气箱,将气流方向转移至轴向。电机转速为990 r/min,设计流量为240.2m3/s。
图1为引风机的平面示意图,图中示出了几个主要部件,包括进气箱、动叶以及前后导叶等。图2为数值计算的模型图,为了便于网格离散,沿着流线方向将整个区域分成了6个计算域。
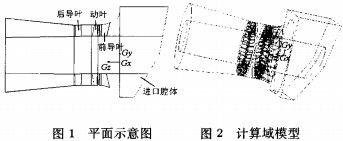
3、数值分析方法
数值计算选用Realizable湍流模式来封闭Reynolds时均N-S方程。采用的离散方法是有限体积法,以此来将控制方程转化为能够数值求解的离散代数方程,其中动量、湍动能、湍流耗散等均采用二阶迎风差分格式离散。这些方程采用分离隐式法求解,通过SIMPLE算法来耦合压力与速度。考虑到气流的最大线速度及密度变化,气流采用可压缩处理。选用的边界条件为质量进口和压力出口。
引风机计算域全部采用非结构化网格,初始网格数目为100万,这给求解过程中基于一定求解结果的冈格自适应留下了适量的细化空间。经过自适应后的网格数目在160万左右。对于如此之多的网格数目,为了缩短计算时间,本文运用了并行计算。单机计算每步耗时3分钟,两台同样配置的计算机并行计算每步耗时不到1分钟,并行优势明显。求解过程中,当残差减小至10_4量级以下且计算域进出口质量流量误差小于O.l%时认定收敛,此时的计算数据可用于结果分析。
4、内流结果分析
4.1进气箱的影响
风机前置进气箱会增大叶轮进口和轮毂面附近的湍流度,使内流场不稳定性增大。所以有必要对其流动情况进行分析,进气箱中良好的出流条件会明显改善下游的流场结构。
图3为进气箱中不同位置截面上的矢量图,图中显示,竖直方向的来流在向着轴向过渡的过程中对轴套产生了较大的冲击,局部损失比较大。图4为气流绕流轴套的流线图。竖直方向的来流在遇到轴套后,大部分气流直接作90°的拐弯,方向转至轴向,少部分气体绕过轴套后从轴套下方转至轴向,这样一来,势必引起经过进气箱后流动的周向不均。
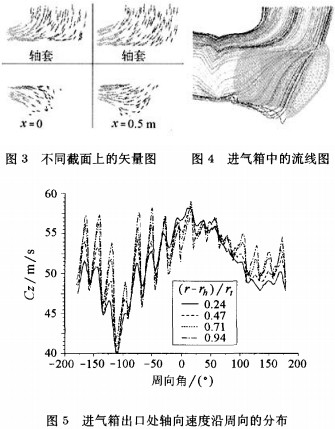
图5给出了进气箱出口不同径向位置处气流的轴向速度沿周向的分布。从图中可以发现,轴向速度出现明显的周向不均,随着半径的增大,轴向速度略微呈现出上升的趋势。这种明显的不均匀作用到下游的旋转部件上,会使得叶道流量出现明显的周向不均,这会造成流入叶道的气流攻角周向不均。对于叶轮这一旋转部件而言,这种周向不均实质上表现为每个叶片上所受的载荷出现周期性的变化,这种强烈的变化可能诱发叶片大的振动,影响气动性能、降低部件寿命。
因此可以通过适当调整轴套的尺寸和改进进气箱的几何结构来改善进气箱中的流动情况。另外,不均匀性对下游流动部件影响的定量分析和在进气箱中配备性能较好导叶以改善不均匀性等方面的问题有待进一步研究。
4.2进口预旋的影响
本文对叶轮进口正负预旋和无预旋情况下的数值计算结果进行了对比,其中正负预旋方案的预旋角分别为200和-200。在下面的研究分析中,定义rt为叶高,th为轮毂半径。
图6为三种不同方案叶轮进出口处周向速度沿径向的分布。叶轮进口处,零预旋情况下,周向速度分布均匀,速度几乎为零;而负预旋时,速度分布沿着翼展方向略微呈现出一定的上升趋势,其值维持在-60 m/s左右;在正预旋时,速度沿着翼展方向呈现递减趋势。叶轮出口处,零预旋时速度分布依然比较均匀,其值在50 m/s附近;而负预旋中不同径向位置的周向速度变动较大;正预旋进出口处的速度分布差不多。相比之下,正预旋方案时叶轮的做功能力最差;负预旋方案下的做功能力较零预旋更强。
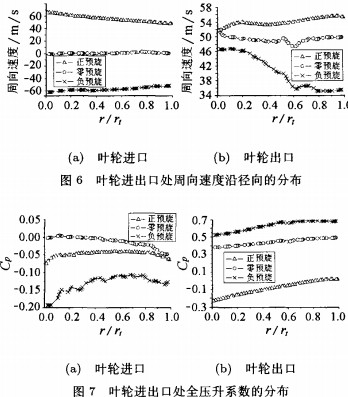
给定全压升系数的计算公式:Cp=△p/(0.5pC2)。图7为三种方案中叶轮进出口处的全压升系数分布。在叶轮进口处,从图中可以看出进口预旋形式较大的影响了引风机进口段的损失。其中,负预旋时总压系数沿径向的变动最为明显,而且值最小。叶轮出口处,总压升沿着翼展均呈现缓慢的增加趋势。三种方案均显示出沿着翼展方向叶片的做功能力相当。
通过比较表明,负预旋虽然加大了叶轮对气体的做功量,同时也明显增大了进口段全压损失且恶化了流场结构。这和文献中的实验结论相符。
4.3前导叶位置的影响
从叶片部件出来的气流,其湍流强度肯定有所加强,如果没有足够的衰减空间,在进入下一个叶片部件时势必会影响其效率,所以叶轮间距不宜太小,小的间距将导致气动噪声增加;当然间距也不宜大,因为大的间距会增大风机的轴向尺寸。
基于这些因素,该部分比较了带负预旋的前导叶在距离动叶不同轴向位置时的性能,如图8所示。随着前导叶和动叶的间距增加,风机压升逐渐减小;而其效率呈现出先增加后减小的态势,因为在小间距情况下,动叶与静叶之间一定程度上的干涉影响了气动性能,当间距增加到一定程度时,继续增加,相应地增加了沿程损失。
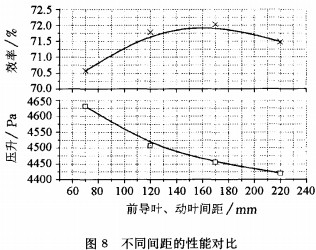
图9是前导叶和动叶间距分别为170 mm和70mm两种方案时竖直平面上的湍流强度分布。相比图9(a),图9(b)中由于前导叶和动叶的间距较大,使得从前导叶流出气体的湍流强度有更大衰减空间,因此其湍流强度的分布更为均匀,而且湍流强度值更小,流动结构更好,这和图8所表现出来的外特性是吻合的。
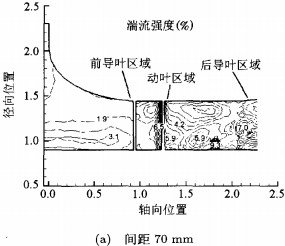
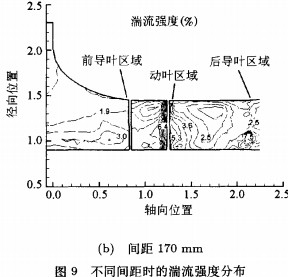
纵观整个流动区域,两种方案中的湍流强度沿流线方向均表现出了相同的演变规律。由于进气箱结构的复杂性,气流经过后湍流强度有所加强。在前导叶区域,湍流强度逐渐增大,其梯度方向基本上沿着流动方向。在动叶中,湍流强度的变化剧烈,在出口下游的轮毂处出现最大值,图9(a)中最大值的位置要靠前。另外,后导叶和动叶间的距离较大,这样的布置是保证从叶轮出来的高湍流强度的气流有足够的衰减距离,从而避免在后导叶进口处出现较大的流场波动和噪音。
5、性能对比
本文将带前后导叶的设计方案在不同工况点的数值计算的性能曲线与实验数据进行了对比,如图10所示。
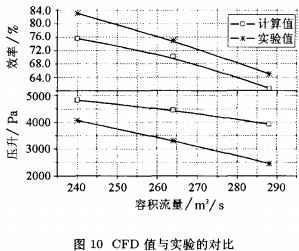
图中显示数值计算的压力值较实验值高,效率值要低,变化趋势一致。这有可能为数值计算中动叶的安装角和实验中的偏差所致。另外,在前、后导叶的处理上,数值计算中对几何模型作了一定的近似处理,这也是引起差别的原因之一。随着接下来在轴流引风机中数值计算自身的不断完善,以及数值计算的计算模型与实物模型的更接近,两种结果会更加符合。
6、结 论
本文对带有前后导叶和复杂进气箱的轴流引风机进行了全三维的数值计算,其间采用了网格自适应和并行计算的技术,力求更为合理地利用计算资源,提高计算的速度和精度。本次计算较好地捕捉到了轴流引风机中一些重要的流动特征,得出了一些有价值的流动结构。这些现象充分说明风机内部流动结构非常复杂,而且部件之间的相互关联非常紧密。
(1)复杂进气箱中的流动状况不甚理想,其复杂的形状和不合理的轴套结构会增大流动的不稳定性和损失,并引起了下游流动的周向不均匀性,这种不均匀性会影响下游叶轮流道中的流量不均,从而引起每个叶片所受的载荷发生周期性的变化,这种强烈的变化可能诱发叶片大的振动,影响气动性能、降低部件寿命。开展对进气箱形状和轴套结构的改进工作有必要。
(2)通过对比不同的预旋方案,发现在零预旋情况下叶片翼展方向上各处的做功能力相当,而且进气段损失小;正预旋下的做功能力最小;负预旋方案虽然加大了叶轮对气体的加功量,同时也明显增大了进口段全压损失且恶化了流场结构。
(3)研究了前导叶位置对流动、性能的影响,通过对比得到了相对合理的前导叶位置。
三门峡富通新能源销售颗粒机、风机、轴流风机、离心风机等机械设备。







